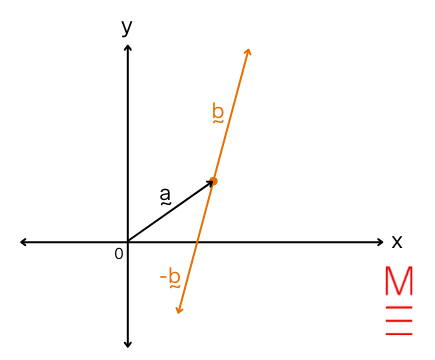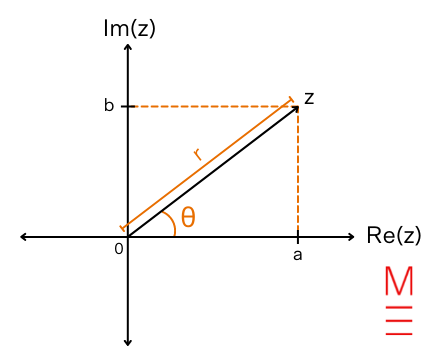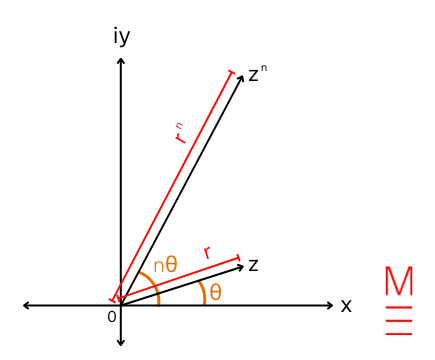The NESA Maths Reference Sheet is a good useful resource… if you understand how to make use of it! Navigate vectors, advanced numbers and mechanics with our Final NESA Maths Reference Sheet Information.
Whereas memorisation has its place in studying, Matrix recommends that college students be taught to derive their responses and learn to apply these formulae appropriately. As a bonus, we’ve included a nifty HSC Maths Cheatsheet so that you can obtain and print out!
Click on on the next formulation to see what they imply and apply them to a observe query!
| Vectors |
| ( |{bf u}|=|x{bf i}+y{bf j}|=sqrt{x^2+y^2} )
({bf u} cdot {bf v} = |{bf u}||{bf v}|textual content{cos} theta = x_1 x_2 + y_1 y_2 , ) start{align*} ({bf r}={bf a} + λ {bf b}) |
Maths Extension 2 solely:
| Advanced Numbers |
| (z=a+ib)
(z=r( textual content{cos} theta +i textual content{sin} theta) ) (z= re^{i theta}) ([r( text{cos} theta + i text{sin} theta )]^n) |
| Mechanics |
| (frac{d^2x}{dt^2} = frac{dv}{dt} = v frac{dv}{dx} = frac{d}{dx} left( frac{1}{2} v^2 proper))
(x=a textual content{cos} (nt+α)+c) (x=a textual content{sin} (nt+α)+c) ( ddot x= -n^2(x-c)) |
Vectors
| Use | Components | Clarification |
| Magnitude of the vector | ( |{bf u}|=|x{bf i}+y{bf j}|=sqrt{x^2+y^2} ) | start{align*} |{bf u}| &= textual content{size/magnitude of }{bf u} (x, y) &= textual content{ Cartesian coordinates of place vector } {bf u} {bf i}&: textual content{ unit vector within the course of the x-axis} {bf j}&: textual content{ unit vector within the course of the y-axis} finish{align*} 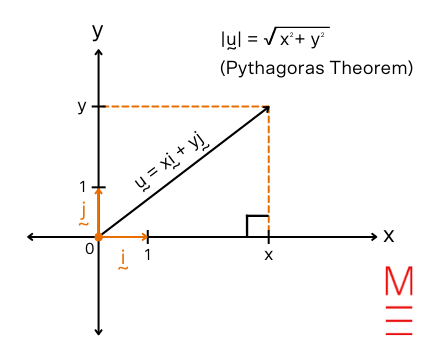 |
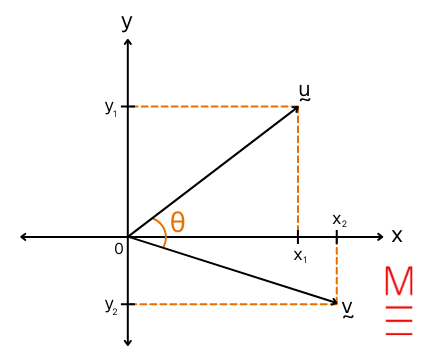
| Dot product | ({bf u} cdot {bf v} = |{bf u}||{bf v}|textual content{cos} theta = x_1 x_2 + y_1 y_2 , )start{align*} textual content{the place } {bf u} &= x_1 {bf i} + y_1{bf j} textual content{and } {bf v} &= x_2{bf i} + y_2{bf j} finish{align*} |
 |
| Vector type of a line | ({bf r}={bf a} + λ {bf b}) | A line will be expressed in many various kinds like Cartesian type ((y =mx+c)) and vector type.
Once we specific line ({bf r}) in vector type, we describe it utilizing a degree ({bf a}= binom{x}{y}) that it passes via and its gradient vector ({bf b}). By substituting completely different fixed values for (λ∈R), the vector equation ({bf r}={bf a} + λ {bf b}) describes each single level on line ({bf r}).
|
Again to prime
Instance 28:
Categorical the road y = 4x + 3 in vector type.
Resolution 28:
| Discover a level that y = 4x + 3 passes via:
start{align*}
Discover a gradient vector of the road y = 4x + 3: For the reason that equation of the road is within the type y = mx + c, the gradient is the coefficient of x. start{align*} Now that we all know that the road passes via (binom{1}{7}) and has a gradient vector of (binom{1}{4}), we are able to specific the road in vector type: ({bf r}= binom{1}{7} + λ binom{1}{4}) the place (λ∈R) |
Again to prime
Maths Extension 2 solely:
Advanced Numbers
| Use | Components | Clarification |
| Cartesian type | (z=a+ib) | (z) is a fancy quantity that may be expressed in many various kinds.
start{align*} r &= |z| = textual content{modulus or size of z}
|
| Polar type | (z=r( textual content{cos} theta +i textual content{sin} theta)) | |
| Euler’s method | (z=re^{i theta}) | |
| De Moivre’s Theorem | start{align*} [r( text{cos} theta + i text{sin} theta )]^n &= r^n (textual content{cos} n theta + i textual content{sin} n theta) &= r^n e^{in theta} finish{align*} |
The argument of (z^n) is n instances as massive because the argument of (z) .
i.e. ( Arg(z^n)= textual content{n}Arg(z) ) The modulus of (z^n) is the same as the modulus of (z) to the ability of (n) . i.e. ( |z^n|= |z|^n )
|
Again to prime
Mechanics
| Use | Components | Clarification |
| Manipulating expressions for acceleration, velocity and displacement | (frac{d^2x}{dt^2} = frac{dv}{dt} = v frac{dv}{dx} = frac{d}{dx} left( frac{1}{2} v^2 proper)) | Need assistance understanding differentiation?
See the next Maths Guides! Maths Adv Functions of differentiation Maths Ext 1 Functions of differentiation (Yr 11) Differential equations |
| Expression for displacement (x) when it comes to time (t) | (x=a textual content{cos} (nt+α)+c) | start{align*} x & = textual content{displacement} frac{2pi}{n} &= textual content{Interval} |
| (x=a textual content{sin} (nt+α)+c) | ||
| Expression for acceleration ( ddot x) when it comes to displacement (x) | ( ddot x= -n^2(x-c)) | (ddot x = textual content{acceleration}) |
,